Estuarine circulation
Definition of Estuarine circulation:
Residual flow pattern in an estuary induced by the density difference between seawater and river water.
This is the common definition for Estuarine circulation, other definitions can be discussed in the article
|
Contents
Introduction
Seawater has a higher density than river water, due to its high salinity (see the article Seawater density). The density difference is of the order of 2.5%. In estuaries where seawater and river water meet, seawater will tend to intrude beneath the river outflow. Part of the intruding seawater will mix with river water, whereby seawater is returned to the sea by estuarine outflow in the upper water layer. This allows 'new' seawater to enter the estuary via the lower water layers. In this way, a circulation of seawater is created, which is directed inland along the bottom and seaward along the surface, see figure 1. This circulation is called estuarine circulation or gravitational circulation. It is driven by the longitudinal density gradient along the estuary: higher-density seawater water in the downstream part of the estuary 'diving' under lower-density mixed water in the inner estuary. The circulation is kept going by mixing of seawater with outflowing river water. Mixing is the result of turbulence, which in estuaries is mainly caused by strong tidal flows. Most of the mixing takes place vertically in the water column due to turbulence generated by tidal flow along the estuarine bottom[1]. The different processes that drive estuarine circulation are discussed in this article. In estuaries with little tide there is hardly any mixing of seawater with river water. In that case a more or less stationary salt wedge forms along the bottom; this case is discussed in the article Salt wedge estuaries.
The classical theory
The classical theory of estuarine circulation was first developed by Hansen and Rattray in 1965 [2], after earlier investigations by D. Pritchard in the St. James river [3]. Many other authors have subsequently contributed to further verification and refinement[4][5].
In the classical theory of estuarine circulation, advection of seawater up and down the estuary by the tidal motion and associated mixing processes are not considered explicitly. This theory considers a stationary salinity field in a frame that moves cyclically up and down the estuary while vertical mixing processes are represented by a tide-averaged and depth-averaged diffusivity. The role of tidal motion is reduced to the generation of turbulence at the channel bed, which produces turbulent eddies that exchange of mass and momentum across the water column.
Nowadays, the intrusion if seawater in an estuary can be simulated in numerical models that incorporate detailed descriptions of turbulent exchange processes and complex bathymetries, see for example Scott (1994)[6], Jay and Musiak (1996)[7] and Burchard et al. (2011)[8]. However, insight in the seawater intrusion process and some rough estimates of the contribution of estuarine circulation can already be obtained from the classical analytical approach. It shows the important role of density stratification for the suppression of turbulent vertical mixing. In the case of weak stratification and strong vertical mixing the river discharge opposes the intrusion of seawater. The strength of the estuarine circulation increases with increasing river discharge whereas the seawater intrusion length decreases. In the case of strong stratification and resulting suppression of turbulent mixing, the strength of the estuarine circulation depends primarily on the tidal velocity. Seawater intrusion related to estuarine circulation strongly decreases with increasing tidal velocity, but increases with increasing river discharge (increase relative to tidal discharge amplitude). This counterintuitive result of the model can be explained by tilting of the pycnoclines due to the increase of stratification and decrease of internal friction. It should be emphasized that the validity of these results requires that the conditions for the validity of the classical analytical model are satisfied (in particular a river discharge much smaller than the tidal discharge amplitude, also in the case of strong stratification – see the appendix). An important limitation of the validity of the classical tide-averaged model is due to ignoring the difference in stratification between ebb and flood, as explained in the next section.
The classical tide-averaged model is presented in the appendix, together with a numerical example. Observed salt intrusion lengths are typically several times larger than the estimate from the analytical model. This can be explained by the neglect of other processes that also contribute to seawater intrusion. The analytical model is a strong simplification of reality. The prismatic channel approximation and the tidal averaging preclude important seawater intrusion mechanisms, such as:
- dispersion by horizontal tidal shear effects and by horizontal residual circulations;
- dispersion by horizontal residual circulations related to the flow structure in channel bends;
- dispersion related to estuarine geometrical characteristics such as secondary channels and tidal flats ('dead zones');
- dispersion related to the chaotic nature of water parcel trajectories.
Seawater intrusion produced by these dispersion mechanisms is discussed in the article Seawater intrusion and mixing in estuaries.
Asymmetric Tidal Mixing
In 1986, Van Aken [9] explained the onset of seasonal stratification in the North Sea by the process of tidal advection of surface water with lower density, related to the presence of strong salinity gradients. A few years later, Simpson et al. [10] observed and modelled tidal variation of stratification in Liverpool Bay by this differential advection mechanism, which they called "tidal straining". Observations by Stacey and Ralston (2005)[11] and numerical model studies by Jay and Musiak[7] and Scott[6] revealed that tidal straining can strongly influence estuarine circulation. When during flood high salinity seawater enters the estuary, the less dense estuarine surface water is repulsed, leading to more upright pycnoclines. The density gradient generates an additional acceleration of the near-bed flow relative to the surface flow. The strong near-bed turbulence generated by bed shear stress during flood reduces stratification by the entrainment of surface water into the near-bed layer[12]. Further reduction of density stratification can be achieved by so-called 'convective overturning': seawater being advected by tidal flow on top of less dense estuarine water[13]. During ebb, surface slope and density gradient exert opposing forces to the near-bed flow. Seaward flow of less dense estuarine water is concentrated near the surface, while momentum exchange between surface and near-bed flow is reduced due to increased stratification, see figure 2. The net effect of asymmetric tidal mixing is an enhancement of the tide-averaged landward near-bed flow, as confirmed by numerical experiments [14]. Asymmetric tidal mixing also induces a positive correlation between vertical gradients in velocity and salinity over the tidal cycle, thus implying a stronger up-estuary salt flux than given by the classical tide-averaged model.
Enhancement of estuarine circulation by asymmetric tidal mixing only occurs in situations of weak-moderate stratification. In case of strong stratification (weak tides, high river runoff) momentum exchange between surface and near-bottom water hardly occurs (see Salt wedge estuaries). Numerical modelling suggests that the relative importance of estuarine circulation by asymmetric tidal mixing (compared to the density-driven flow) decreases as stratification increases[15]. Enhancement of estuarine circulation by asymmetric tidal mixing is strongest for small Richardson numbers (typically [math]Ri \lt 1[/math], see appendix) and periodic or weak stratification.
Reversal of tidal mixing asymmetry can occur during the spring-neap tidal cycle, as observed in the well-mixed Gironde estuary[16] (spring tidal range 5 m, neap tidal range 2.5 m). Whilst at spring tide, bottom-generated turbulence during flood is stronger than during ebb, the opposite occurs at neap tide. At neap tide, vertical mixing during flood tide is suppressed by enhanced stratification, limiting the extent of the bottom boundary layer and producing a subsurface flood velocity maximum[17].

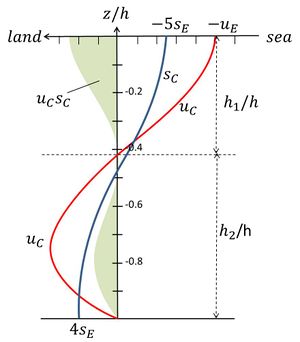
Figure 3 illustrates asymmetric tidal mixing in Rotterdam Waterway. The velocity and salinity profiles were measured on 9 September 1967 at an estimated net discharge of about 1000 m3/s (runoff velocity [math]u_R \approx 0.2 m/s[/math]). The Richardson number (Eq. 10) has a characteristic value of the order of [math]Ri \approx 1.8[/math]. The sections at maximum ebb and maximum flood flow display asymmetry between near-bottom flow velocities; near-bottom velocities are substantially higher during flood than during ebb (as schematically depicted in figure 2). The sections at H.S.W. and L.S.W. show asymmetry in stratification: at the end of the flood the water column is less stratified than at the end of the ebb. Another survey in Rotterdam Waterway was conducted by De Nijs et al. in 2006 at higher river discharge (stronger stratification) [18]. These authors show that in Rotterdam Waterway asymmetry in tidal mixing is primarily related to asymmetry of the tide at the mouth (faster tidal rise than tidal fall, which enhances flood currents over ebb currents), more than to differential advection. This is consistent with the fast thickening of the bottom boundary layer during flood, caused by strong bed-generated turbulence. A similar behaviour was observed in the Hudson estuary [19].
The previous discussion illustrates that, even in prismatic channels, estuarine circulation is influenced by several important processes which are not included in the classical tide-averaged theory. These processes can be simulated in numerical models in which the turbulent exchange processes of momentum and salinity and the evolution of vertical profiles of velocity and salinity are modelled as mutually dependent processes. These processes, which include asymmetric tidal mixing, tidal straining and convective overturning, and other nonlinear phenomena, are referred to as 'eddy viscosity-shear covariance' (ESCO). They modify substantially the simple picture of density driven estuarine circulation of the classical theory[15][20][21].
Lateral estuarine circulation
In natural estuaries, the depth decreases towards the lateral boundaries (in a meander the depth decreases from the outer bend towards the inner channel bend). Tidal velocities are lower near the channel banks than at the channel centre. The salinity front is therefore not advected at the same speed at different lateral locations. This results in lateral salinity gradients. During flood (especially shortly before the end of the flood phase) the salinity is higher at the channel centre than near the channel banks. During ebb the situation is reversed; near the surface, the salinity at the channel centre is lower than near the channel banks. The lateral salinity gradients related to this differential tidal salinity advection, induce a baroclinic (density-driven) lateral current. This current has a vertical structure; during flood it is directed near the bottom toward the channel banks and toward the channel centre near the surface, see figure 4. The resulting flow convergence at the channel centre is often visible in the field by a scum line following the channel axis [22]. During ebb the lateral exchange flow is divergent at the surface and convergent near the bottom. This lateral baroclinic exchange flow has important consequences for longitudinal dispersion in natural estuaries, as first pointed out by R. Smith [23] and explained in the article Seawater intrusion and mixing in estuaries.
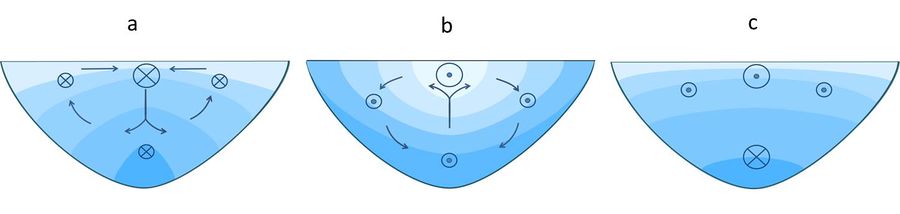
Lateral exchange flows also influence estuarine circulation. Downwelling flow at the channel axis during flood transports momentum down the vertical; surface flow is decelerated and near bottom flow accelerated in up-estuary direction. During ebb, vertical momentum transport reduces turbulent momentum dissipation by reducing the vertical shear of the tidal current. This also favours the baroclinic flow component[24][25]. Lateral baroclinic exchange flow therefore enhances estuarine circulation. It also induces an a net downstream flow component in the shallower parts of the cross-section (lateral inflow of down-estuary momentum from the channel centre during ebb, outflow of up-estuary momentum toward the channel centre during flood, see figure 4); this flow component enhances the down-estuary flow component related to river runoff [8].
Other lateral circulation patterns
Several mechanisms can alter the symmetric flow pattern of figure 5. In wide estuaries the symmetry is broken by earth's rotation. Currents are deviated to the right on the northern hemisphere and to the left on the southern hemisphere (see Coriolis acceleration). Looking in up-estuary direction, flood currents are concentrated at the right side of a straight tidal channel and ebb currents at the left side (northern hemisphere). Estuarine circulation is influenced by earth's rotation in a similar way [26]: the residual up-estuary flow is shifted to the right bank and the down-estuary flow to the left bank, see figure 5. The mean cross-sectional salinity distribution is tilted accordingly.
Channel meandering induces transverse circulation, directed to the inner channel bend in the lower part of the vertical and to the outer bend near the surface. The spiraling tidal flow modifies the salinity distribution and the density-driven longitudinal residual flow in a similar way as earth's rotation when the tidal flow follows a channel meander with the inner channel bend at the right bank [27]. For an inner channel bend at the left bank the picture is mirrored; in this case the effects of channel meandering and earth's rotation are opposite. Channel bends and other topographic structures (bars, shoals) generate longitudinal circulating flow patterns in estuaries also in the absence of density differences. These horizontal topographically induced flow circulations are often stronger than horizontal estuarine circulation generated by density gradients. However, residual flow circulation in the longitudinal-vertical plane is mainly due to the density difference between seawater and river water.
Consequence of estuarine circulation
Estuarine circulation is highly relevant for transport of fine sediments and sedimentation (see Dynamics of mud transport). The up-estuary near-bottom flow captures a substantial part of the downstream flux of fluvial sediment, and moves this sediment back toward the tip of the salt intrusion zone. The up-estuary near-bottom flow contributes also to import of marine sediment into the estuary. This sediment settles on the bed during periods of neap tide and slack water. It is resuspended in periods of high tidal currents, leading to a strong increase in turbidity. Decomposition of organic material in the high turbidity zone can cause oxygen depletion, especially in the lower part of the vertical where mixing with oxygen-rich surface water is inhibited by stratification. However, estuarine circulation is not the only cause of up-estuary sediment transport. Many field and model investigations show that tidal asymmetry due to non-linear tidal propagation in shallow water (leading to stronger flood currents than ebb currents and longer high-water slack periods than low-water slack periods) is often a more important mechanism, see the articles Estuarine turbidity maximum and Tidal asymmetry and tidal basin morphodynamics.
Appendix
In this appendix the classical analytical model for estuarine circulation is presented. The model applies to a straight prismatic estuary (uniform depth [math]h[/math] and width [math]b[/math] ); the width is small enough for neglecting the influence of earth's rotation (Rossby radius [math]U/fb \lt \lt 1[/math] ).
The following notations are used (see also figures 1 and A1):
- [math]x[/math] is the coordinate along the estuarine axis ([math]x=0[/math] at the sea boundary, [math]x=L[/math] at the landward boundary of salt intrusion);
- [math]u[/math] is the velocity in the [math]x[/math]-direction, [math]u(z) = u_R + u_C(z) + U \cos \omega t,[/math] where [math]u_R[/math] is the velocity related to river runoff (river discharge divided by estuarine cross-section), [math]u_C(z)[/math] is the estuarine circulation, [math]U[/math] is the depth-averaged tidal velocity amplitude and [math]\omega = 2 \pi / T[/math] is the tidal radial frequency;
- [math]S=s/s_0[/math] is the ratio of the local salinity [math]s[/math] and the seawater salinity [math]s_0 :[/math] [math]S[/math] is related to the density [math]\rho[/math] by the relation [math]\rho=\rho_0(1+\beta s_0 S),[/math] where [math]\rho_0[/math] is the fresh water density and the expansion coefficient [math]\beta=7.7 \times 10^{-4};[/math]
- [math] p(z) = g \int_z^\eta \rho dz[/math] is the hydrostatic pressure; [math]\eta[/math] is the surface elevation relative to a horizontal plane and [math](-z)[/math] is the depth relative to the surface;
- [math]K_M[/math] is the eddy viscosity (vertical momentum diffusion coefficient [math][m^2/s] [/math] ) and [math]K_S[/math] the eddy diffusivity (vertical salinity diffusion coefficient).
Depth-averaging is denoted by an overbar.
The model
The model is based on the following simplifications:
- The diffusion coefficients [math]K_M, K_S[/math] do not depend on the spatial and temporal coordinates [math]x,z,t[/math] ; this means that the classical model is realistic only for continuously stratified estuaries (no layered salinity structure; such estuaries are often called "well-mixed", see figure A1);
- The estuarine geometry is represented by a prismatic channel;
- The river flow velocity [math]u_R[/math] and the tidal velocity amplitude [math]U[/math] do not depend on the spatial coordinates [math]x,z[/math] ;
- The river flow velocity is at least an order of magnitude smaller than the tidal velocity, [math]u_R \lt \lt U[/math] ;
- The water surface variation is much smaller than depth, [math]\eta \lt \lt h[/math] ; Stokes drift is neglected;
- The vertical flow velocity [math] w[/math] is neglected;
- Side wall effects are neglected, implying uniformity of all variables in lateral [math]y[/math]-direction;
- Longitudinal gradients in the velocity [math]u[/math] are neglected;
- The longitudinal salinity gradient is the same at all depths ([math]\large\frac{\partial S}{\partial x}\normalsize=\large\frac{\partial \overline S}{\partial x}\normalsize ).[/math]
Because of these simplifications, the classical analytical model is not reliable for predicting seawater intrusion into real estuaries. In particular, the first and second simplifications violate the conditions that are representative of real estuaries and imply that important mechanisms for seawater intrusion are ignored, as discussed above. The importance of the classical analytical model lies in the simple illustration it offers for one of the major processes responsible for seawater intrusion into estuaries.
We consider the influence of a constant river flow [math]u_R[/math] on the salinity distribution in a frame moving with the velocity [math]u_R + U \cos \omega t[/math]. In the moving frame the velocity [math]u[/math] is time-independent and depends only on the vertical coordinate [math]z[/math]; we thus have [math]u=u_C(z)[/math]. The only driving force acting on the fluid in the moving frame is the pressure gradient [math]\partial p / \partial x [/math], which is a linearly increasing function of depth ([math]-z[/math]) below mean water level:
[math]\large\frac{1}{g \rho} \frac{\partial p}{\partial x}\normalsize = \large\frac{\partial \eta}{\partial x}\normalsize + (\eta -z) \beta s_0 \large\frac{\partial S}{\partial x}\normalsize . \qquad (1) [/math]
The fluid acceleration caused by this pressure gradient is balanced by momentum dissipation through turbulent diffusion:
[math]\large\frac{\partial p}{\rho \partial x}\normalsize = \large\frac{\partial }{\partial z}\normalsize ( K_M \large\frac{\partial u_C}{\partial z}\normalsize) . \qquad (2) [/math]
This equation can be solved considering the boundary conditions:
No slip at the bottom: [math]u_C(-h)=0[/math] , no momentum diffusion through the surface: [math]du_C / dz =0[/math] at [math]z=\eta \approx 0[/math] and no net discharge: [math]\int_{-h}^0 u_C dz =0[/math].
Because the river runoff is constant and the tide cyclic, the salinity distribution should not change with time in the moving frame. However, the estuarine circulation modifies the salinity distribution, because salt advection [math]u_C(z) S(x,z)[/math] has a gradient in [math]x[/math]-direction. According to the classical theory, the salt balance is restored by vertical diffusion of salinity:
[math]u_C \large\frac{\partial \overline S}{\partial x}\normalsize = \large\frac{\partial }{\partial z}\normalsize ( K_S \large\frac{\partial S}{\partial z}\normalsize) . \qquad (3) [/math]
This equation can be solved with the boundary conditions: no salt flux through bottom and surface, [math]\partial S / \partial z =0[/math] at [math] z=-h, z=0 .[/math]
The solution of equations Eqs. (1-3) is given by (shown in figure A2):
[math] u_C(z)=u_E (-1+9 \zeta^2+8 \zeta^3) , \; S=\overline S + s_C(z), \; s_C(z)=S_E (-5+30 \zeta^2-45 \zeta^4-24 \zeta^5), \; \zeta=z/h , \qquad (4) [/math]
[math]u_E=-\large\frac{c^2 h^2}{48 K_M} \frac{\partial \overline S}{\partial x}\normalsize , \quad S_E=-\large\frac{h^2 u_E}{60 K_S} \frac{\partial \overline S}{\partial x}\normalsize ,\qquad (5) [/math]
where [math] c=\sqrt{\beta s_0 gh} [/math] is twice the maximum internal wave speed in a layered channel with density difference [math]\beta s_0[/math] and total depth [math]h[/math].
Salt balance
The motion in the moving frame is not exactly cyclic; after one tide the moving frame has moved seaward over a distance [math]T u_R[/math] . In order to prevent complete flushing of the salinity a net landward salt transport should exist. Many seawater intrusion mechanisms can contribute to landward salt transport, as discussed in the article Seawater intrusion and mixing in estuaries. In this case, we assume that estuarine circulation is the primary mechanism for seawater intrusion. This means that the loss of salt content from the estuary due to the net shift of the moving frame (moving from any start position in the estuary), [math]hu_rS[/math], should be compensated by salt transport related to estuarine circulation:
[math]h u_R \overline S = \int_{-h}^0 u_C(z)S(z) dz. \qquad (7) [/math]
This balance equation holds for all cross-sections [math]x[/math] landward of the estuarine mouth. Using Eqs. (4, 5) this equation can be rewritten as a nonlinear differential equation for the depth-averaged salinity
[math]\overline S(x) =- ( L \large\frac{d \overline S}{dx} )^3 \normalsize , \quad [/math] with solution [math]\overline S(x) = (1 - \large\frac{2x}{3L})^{3/2}\normalsize , \qquad L \approx 0.024 h^2 c (\large\frac{c}{u_R K_S K_M^2})^{1/3}\normalsize . \qquad (8) [/math]
This equation shows that [math]-1/L[/math] is a fair estimate for the salinity gradient [math]d \overline S / dx[/math] due to estuarine circulation in the range [math]0 \le x \le L/2[/math]. Substitution in Eq. (5) gives the maximum estuarine circulation velocity [math]u_E[/math]:
[math]u_E \approx 0.87(u_R c^2 \large\frac{K_S}{K_M})^{1/3}\normalsize, \quad S_E \approx 0.6 \large (\frac{u_R}{c})^{2/3} (\frac{K_M}{K_S})^{1/3} \normalsize . \qquad (9) [/math]
Estuary number
The estuary number [math]E[/math] was introduced in 1966 by Harleman and Abraham[28] to provide a rapid estimate for the degree of stratification of an estuary. It is defined as
[math]E=\Large\frac{ \mathrm{turbulent \, energy \, dissipated \, by \, tidal \, currents \, during \, a \, tidal \, cycle }}{\mathrm{energy \, needed \, for \, vertical \, mixing \, of \, river \, water \, spread \, during \, one \, tidal \, cycle \, over \, the \, estuarine \, surface}}\normalsize \equiv \Large\frac{E_{tide}}{E_{river}}\normalsize. [/math]
In formulas:
[math]E_{tide} = \rho b_0 l \int_0^T |u_*^3(t)|dt = \frac{4}{3 \pi} \rho b_0 l T u_{* max}^3 , [/math]
where [math]T[/math] is the tidal period, [math]\rho[/math] the estuarine water density, [math]b_0[/math] is the estuarine width at the mouth and [math]l[/math] is a representative estuarine length scale, for example, the basin length for short estuaries or the convergence length for exponentially converging estuaries ([math]b=b_0 \exp(-x/l)[/math]). The turbulent energy dissipation is represented by [math]\rho|u_*^3 (t)|[/math], where [math]|u_*(t)| \approx u_{*max}\, |\sin(2 \pi t /T)| [/math] is a measure of the turbulent velocity fluctuations. The turbulent velocity fluctuations are a fraction of the tidal velocity. The proportionality factor [math]\sqrt{c_D}[/math] is of the order of 0.05-0.07 for well-mixed conditions, but smaller for partially mixed or stratified conditions.
[math]E_{river} = g \Large\frac{\Delta \rho}{2} \frac{h}{2}\normalsize T Q_{river} ,[/math]
where [math]\Delta \rho[/math] is the density difference sea water-river water (which is assumed twice the difference estuary water – river water), [math]Q_{river}[/math] is the river discharge.
The estuary number is then given by
[math]E = \Large\frac{16}{3 \pi}\frac{\rho}{\Delta \rho} \frac{b_0 l u_{*max}^3}{gh Q_{river}}\normalsize .[/math]
Estuaries where [math]E[/math] is at least an order of magnitude larger than 1 are well mixed. Estuaries where [math]E \lt 1[/math] are stratified. Estuaries are partially mixed when [math]E[/math] is less than an order of magnitude larger than 1.
Stratification
Turbulent mixing over the water column is suppressed by the effect of density stratification, also in the case of continuously stratified (non-layered) systems. This implies that the diffusion coefficients [math]K_M, K_S[/math] depend not only on the turbulence generated by the tidal flow, but also on the damping by stratification. This dependence can be related to the so-called Richardson number, [math]Ri= - \large \frac{g}{\rho} \frac{\partial \rho / \partial z}{(\partial u /\partial z)^2} \normalsize[/math].
In accordance with the strong assumption underlying the classical model (well mixed, continuously stratified estuaries, no layered salinity structure), the Richardson number can be approximated by:
[math]Ri \approx (\large\frac{c}{U})^2 \normalsize \Delta S , \quad c^2=\beta s_0 gh , \quad \Delta S = 9 S_E , \qquad (10)[/math]
see figure A2. For small Richardson numbers (typically much smaller than 0.25) the diffusion coefficients are not strongly influenced by vertical density gradients. In this case an estimate of the turbulent diffusion coefficients is given by [math]K_M \approx K_S \approx K = c_D hU[/math]. The friction coefficient [math]c_D[/math] is of the order of 0.001 – 0.004 [29]. Substitution in the expressions for [math]L[/math] (Eq. 8), [math]u_E[/math] (Eq. 9) and [math]S_E[/math] (Eq. 9) yields
[math] u_E \approx 0.87 (u_R c^2)^{1/3} , \; \Delta S \approx 5.4 (\large\frac{u_R}{c})^{2/3}\normalsize , \; L \approx \large\frac{0.024 h}{c_D}\normalsize (\large\frac{c}{u_R})^{1/3} \frac{c}{U}\normalsize . \qquad (11) [/math]
The estuarine circulation and the stratification increase with increasing river runoff [math]u_R[/math]; they do not depend on the tidal velocity amplitude [math]U[/math]. The seawater intrusion length [math]L[/math] decreases with increasing river runoff and with increasing tidal velocity.
For situations with strong (but continuous non-layered) stratification the Richardson number is larger than 1. In this case one may use the expressions for [math]K_M, K_S[/math] established experimentally by Munk-Anderson [30],
[math]K_M = K(1+10Ri)^{-1/2} \approx 0.316 K Ri^{-1/2} , \; K_S = K (1+3.3Ri)^{-3/2} \approx 0.167 K Ri^{-3/2} , \; K=c_D h U . \qquad (12) [/math]
With these approximations we find
[math]u_E \approx 0.27 U , \; \Delta S \approx 17 \large\frac{u_R}{U}\normalsize , \; L \approx \large\frac{h}{c_D}\normalsize (\large\frac{c}{U})^3 (\frac{u_R}{U})^{1/2}\normalsize . \qquad (13) [/math]
The estuarine circulation [math]u_E [/math] now depends only on the tidal velocity amplitude [math]U[/math] . The situation [math]U=0[/math] corresponds to an arrested salt wedge. However, in this case the present model loses its validity (the bottom-surface salinity difference [math]\Delta S[/math] becomes larger than 1). For a description of the arrested salt wedge the reader is referred to the article Salt wedge estuaries. The present model for estuarine circulation requires [math]u_R \lt \lt U[/math]. Assuming that this condition is satisfied, the seawater intrusion length [math]L[/math] increases with an increase of runoff [math]u_R[/math]. This counterintuitive result can be explained by the fact that the river runoff loses its 'grip' on the near-bottom seawater intrusion with increasing stratification.
Numerical example
Consider an estuary characterized by: [math]U[/math]=1 m/s, [math]h[/math]=10 m, [math]u_R[/math]=0.05 m/s, [math]c_D[/math]=0.002. Using the formulas (13) we find [math]u_E\approx 0.27 m/s, \; \Delta S \approx 0.85, \; Ri \approx 1.7[/math]. An improved estimate can be obtained by using the non-approximated form of Eqs. (12); this yields similar values. The salt intrusion length is given by [math]3L/2[/math] according to Eq. (8). This gives a seawater intrusion length of about 5 km. Taking other dispersion processes into account, in addition to estuarine circulation, the salt intrusion length can be substantially larger. A larger salt intrusion length implies a proportionally smaller estuarine circulation [math]u_E[/math], according to equation (5). Field observations show that the estuarine circulation is of the order of 0.1 m/s and often larger, even when longitudinal and vertical salinity gradients are small. Although the numerical example gives reasonable order of magnitude estimates for the estuarine circulation and the salt intrusion length, the application of the empirical formulas Eq. (12) for the diffusion coefficients requires great caution. Several studies express serious doubts about the general applicability of the mixing length concept, even for well-mixed estuaries[31][32][33].
Related articles
- Salt wedge estuaries
- Seawater density
- Seawater intrusion and mixing in estuaries
- Coriolis acceleration
- Dynamics of mud transport
- Estuarine turbidity maximum
References
- ↑ Trowbridge, J.H., Geyer, W.R., Bowen, M.M. and Williams, A.J. (1999) Near-bottom turbulence measurements in a partially mixed estuary: turbulent energy balance, velocity structure, and along-channel momentum balance. J. Phys. Oceanogr. 29: 3056–72
- ↑ Hansen, D.V. and Rattray M. (1965) Gravitational circulation in straits and estuaries. J. Mar. Res. 23: 104–22
- ↑ Pritchard, D.W. (1952) Salinity distribution and circulation in the Chesapeake Bay estuaries system. J. Mar. Res. 11: 106–23
- ↑ Geyer, W.R., Trowbridge. J.H. and Bowen, M.M. (2000) The dynamics of a partially mixed estuary. J. Phys. Oceanogr. 30: 2035–48
- ↑ MacCready, P. (2004) Toward a unified theory of tidally-averaged estuarine salinity structure. Estuaries 27: 561–70
- ↑ 6.0 6.1 Scott, C.F. (1994) A numerical study of the interaction of tidal oscillations and nonlinearities in an estuary. Estuarine Coast. Shelf Sci. 39: 477–96
- ↑ 7.0 7.1 Jay, D.A. and Musiak, J.D. (1996) Internal tidal asymmetry in channel flows: origins and consequences. In Mixing Processes in Estuaries and Coastal Seas, ed. C Pattiaratchi, Am. Geophys. Union, Washington: 211–49
- ↑ 8.0 8.1 Burchard, H., Hetland, R.D., Schulz, E. and Schuttelaars, H.H. (2011) Drivers of Residual Estuarine Circulation in Tidally Energetic Estuaries: Straight and Irrotational Channels with Parabolic Cross Section. J.Phys.Oceanogr. 41: 548-570
- ↑ Van Aken, H. M. (1986). The onset of seasonal stratification in shelf seas due to differential advection in the presence of a salinity gradient. Cont. Shelf Res. 5: 475-485
- ↑ Simpson, J.H., Brown, J., Matthews, J.and Allen, G. (1990) Tidal straining, density currents, and stirring in the control of estuarine stratification. Estuaries 13: 125-132
- ↑ Stacey, M.T. and Ralston, D.K. (2005) The scaling and structure of the estuarine bottom boundary layer. J. Phys. Oceanogr. 35:55–71
- ↑ Chant, R. J., Geyer, W. R., Houghton, R., Hunter, E., and Lerczak, J. A. (2007). Estuarine Boundary Layer Mixing Processes: Insights from Dye Experiments. Journal of Physical Oceanography 37: 1859–1877
- ↑ Prandle, D. (2004) Saline intrusion in partially mixed estuaries. Estuarine, Coastal and Shelf Science 59: 385-397
- ↑ Burchard, H. and Baumert, H. (1998) The formation of estuarine turbidity maxima due to density effects in the salt wedge. A hydrodynamic process study. J. Phys. Oceanogr. 28: 209–321
- ↑ 15.0 15.1 Cheng P., De Swart, H.E. and Valle-Levinson, A. (2013) Role of asymmetric tidal mixing in the subtidal dynamics of narrow estuaries. J. Geophys. Res. 118: 2623–2639
- ↑ Ross L., Huguenard, K. D. and Sottolichio, A. 2019. Intratidal and fortnightly variability of vertical mixing in a macrotidal estuary: The Gironde. Journal of Geophysical Research: Oceans 124: 2641–2659
- ↑ Chen, W. and de Swart, H. E. 2016. Dynamic links between shape of the eddy viscosity profile and the vertical structure of tidal current amplitude in bays and estuaries. Ocean Dynamics 66: 299–312
- ↑ De Nijs, M.A.J., Pietrzak, J.D. and Winterwerp, J.C.(2011) Advection of the Salt Wedge and Evolution of the Internal Flow Structure in the Rotterdam Waterway. J. Phys. Oceanogr. 41: 3-27
- ↑ Nepf, H.M. and Geyer, W.R. (1996) Intratidal variations in stratification and mixing in the Hudson estuary. J. Geophys. Res. 101: 12079-12086
- ↑ Dijkstra, Y.M., Schuttelaars, H.M. and Burchard, H. 2017. 3. Generation of exchange flows in estuaries by tidal and gravitational eddy viscosity-shear covariance (ESCO). J. Geophys. Res. Oceans 122: 4217–4237
- ↑ Cheng, P., Mao, J., Yu, F., Chen, N., Wang, S. and Fanghua Xu, F. 2019. A numerical study of residual flow induced by eddy viscosity-shear covariance in a tidally energetic estuary. Estuarine, Coastal and Shelf Science 230, 106446
- ↑ Nunes, R.A. and Simpson, J.H. (1985) Axial Convergence in a Well-mixed Estuary. Coastal and Shelf Science 20: 637-649
- ↑ Smith, R. (1976) Longitudinal dispersion of a buoyant contaminant in a shallow channel. J. Fluid Mech. 78: 677–88
- ↑ Lerczak, J. A. and Geyer, W. R. (2004) Modelling the lateral circulation in straight, stratified estuaries. J. Phys. Oceanogr., 34: 1410–1428
- ↑ Burchard, H. and Schuttelaars, H.H. (2012) Analysis of Tidal Straining as Driver for Estuarine Circulation in Well-Mixed Estuaries. J. Phys. Oceanograph. 42: 261-271
- ↑ Huijts, K.M.H., Schuttelaars, B.H.M., De Swart, H.E. and Friedrichs, C.T. (2009) Analytical study of the transverse distribution of along-channel and transverse residual flows in tidal estuaries. Continental Shelf Res. 29: 89-100
- ↑ Basdurak, N.B. and Valle-Levinson, A. (2013) Tidal variability of lateral advection in a coastal plain estuary. Continental Shelf Res. 61–62: 85–97
- ↑ Harleman, D. R. F. and Abraham, G. 1966. One-dimensional analysis of salinity intrusion in the Rotterdam Waterway, Delft Hydraulics Laboratory Publication 44, October 1966
- ↑ Bowden, K.F. 1967. Stability effects on turbulent mixing in tidal currents. Phys. of Fluids 7, S278
- ↑ Munk, W.H. and Anderson, E.R. (1948). Notes on the theory of the thermocline. J. Marine Res. 7: 276-295
- ↑ Uittenbogaard, R.E. 1993. Testing some damping functions for mixing-length turbulence models. Report Delft Hydraulics Z721
- ↑ Nunes Vaz, R.A. and Simpson, J.H. 1994. Turbulence closure modeling of estuarine stratification. Journal of Geophysical Research 99: 16,143-16,160
- ↑ Simpson, J.H., Williams, E., Brasseur, L.H. and Brubaker J.M. 2005. The impact of tidal straining on the cycle of turbulence in a partially stratified estuary. Continental Shelf Research 25: 51–64
Please note that others may also have edited the contents of this article.
|