Data analysis techniques for the coastal zone
This article introduces several data analysis methods commonly used for the interpretation of datasets generated by coastal and marine survey programs. The methods described in this article - linear regression, wavelets, and methods based on principal component analysis - apply to data with uncorrelated measurement errors that are approximately Gaussian-distributed. Another article, Data interpolation with Kriging, deals with the analysis of datasets in which correlations between data biases cannot be ignored. For very large datasets, artificial neural networks are often a suitable analysis tool, see the article Artificial Neural Networks and coastal applications.
Contents
General description
The aim of data analysis methods is generally to find a small number of shape functions or sinusoidal functions, or a small number of eigenvectors, that resolve with sufficient accuracy the spatial and temporal properties of the data. This data may relate to some of the forcings, like the waves, winds and currents, or to the bathymetry. An approximation of the data to about 80% to 85% may be sufficient for some applications and in such cases maybe 2 to 5 functions or eigenvectors may be chosen. However, it is generally preferably to be able to approximate the original data set with at least 90% (Gilmore and Lefranc, 2003)[1], especially when the objective is to find a set of variables embedded in the original dataset, as is the case for some chaotic techniques (described in more detailed below). Nonetheless, in coastal engineering it is common practice to approximate the data of interest with up to 5 functions or eigenvectors (see for example Rattan et al. 2005[2] or Li et al., 2005[3]) in order to simplify the analysis. Such methods are described in more detail below, following the reviews by Southgate et al. (2003) [4] and Larson et al. (2003)[5]. Bulk statistics methods, discussed by Larson et al. (2003), are briefly summarized below. Then follows an analysis methods for beach level data. Finally some advanced linear and nonlinear data analysis methods are presented.
Bulk statistics methods
This method uses the statistical properties of a data time series (mean, range, variance, correlation, etc.) to characterize the behavior of a system. As such, the implementation of the method is very simple, and it has thus been extensively used in many fields, including coastal research. These methods have traditionally been applied to short-term and long-term wave statistics, for instance. In short-term wave analysis, a wave height may be analyzed directly, or after being decomposed in a sum of sinusoidal functions (that is, using a Fourier expansion), from which the moments of the data may be extracted. These methods allow, also, to calculate the properties of extreme events according to their probability of occurrence, and are thus very useful in coastal structure design (Larson et al., 2003[5]). In relation to morphodynamics, statistical properties of the temporal and spatial evolution of different coastal features have been investigated, in particular as a preliminary step in studies when Principal Component Analyses are involved (discussed later).
Linear regression analysis of beach level data
A short introduction to linear regression theory is given in Appendix A.
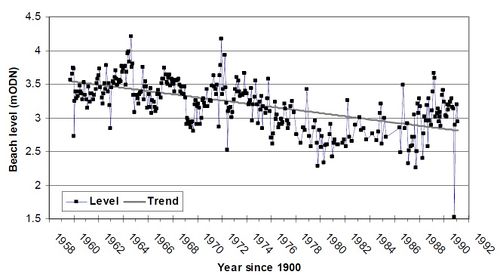
Linear regression analysis of beach level data is demonstrated here using a set of beach profile measurements carried out at locations along the Lincolnshire coast (UK) by the National Rivers Authority (now the Environment Agency) and its predecessors between 1959 and 1991, as described in Sutherland et al. 2007[4]. Locations backed by a seawall were chosen and a time series of beach levels at a set point in front of the seawall at Mablethorpe Convalescent Home are shown in Figure 1.
Use of trend line for prediction
Straight lines fitted to beach level time series give an indication of the rate of change of elevation and hence of erosion or accretion. The measured rates of change are often used to predict future beach levels by assuming that the best-fit rate from one period will be continued into the future. Alternatively, long-term shoreline change rates can be determined using linear regression on cross-shore position versus time data.
Genz et al. (2007)[6] reviewed methods of fitting trend lines, including using end point rates, the average of rates, ordinary least squares (including variations such as jackknifing, weighted least squares and least absolute deviation (with and without weighting functions). Genz et al. recommended that weighted methods should be used if uncertainties are understood, but not otherwise. The ordinary least squares, jackknifing and least absolute deviation methods were preferred (with weighting, if appropriate). If the uncertainties are unknown or not quantified then the least absolute deviation methods is preferred.
The following question then arises: how useful is a best-fit linear trend as a predictor of future beach levels? In order to examine this, the thirty years of Lincolnshire data have been divided into sections: from 1960 to 1970, from 1970 to 1980, from 1980 to 1990 and from 1960 to 1990, for most of the stations. In each case a least-squares best-fit straight line has been fitted to the data and the rates of change in elevation from the different periods are shown below:
- From 1960 to 1970 the rate of change was -17mm/year;
- From 1970 to 1980 the rate of change was -63mm/year;
- From 1980 to 1990 the rate of change was +47mm/year.
- From 1960 to 1990 the rate of change was -25mm/year.
The data above indicates that 10-year averages provide little predictive capability for estimating the change in elevation for the next 10-years, let alone for the planning horizon that might need to be considered for a coastal engineering scheme. Few of the 10-year averages are close to the 30-year average.
A prediction horizon is defined as the average length of time over which a prediction (here an extrapolated trend) produces a better level of prediction of future beach levels than a simple baseline prediction. Sutherland et al. (2007)[4] devised a method of determining the prediction horizon for an extrapolated trend using the Brier Skill Score (Sutherland et al., 2004[7]). Here the baseline prediction was that future beach levels would be the same as the average of the measured levels used to define the trend. A 10 year trend was found to have a prediction horizon of 4 years at Mablethorpe Convalescent Home (Fig. 2). Similar values have been found at other sites in Lincolnshire.
Conditions for application
Assumptions underlying regression analysis and least-square fitting are:
- the deviations from the trend curve can be equated with Gauss-distributed random noise;
- the deviations are uncorrelated.
In the example of Mablethorpe beach the distribution of residual (i.e. de-trended) beach levels seems to follow the common assumption of a Gaussian (normal) distribution, as shown in Fig. 2.
If the data have random fluctuations which are significantly correlated over some distance, other regression methods must be used. Frequently used analysis methods in this case are:
Wavelets
The wavelet technique is similar to a Fourier analysis approach, where the signal is approximated by some basis functions, which in wavelet analysis are simply wavelet functions. The drawback of Fourier analysis or the more general harmonic analysis, in which data are represented by a superposition of sinusoidal terms, is the assumption of cyclicity beyond the spatial or temporal range of the dataset. This assumption may be justified if dominant processes have a linear or weakly non-linear character (see, for example, the article Stability processes), but in practice many morphological features and processes are influenced by highly nonlinear perturbations both in space (e.g., presence of geological sedimentary structures) and in time (e.g., occurrence of extreme storms). In this case no good representation of the dataset can be obtained with a limited number of sinusoidal functions. Wavelets, on the contrary, can represent highly nonlinear behavior and do not assume any cyclicity, as they are localized in space and in time (Burrus et al., 1998[8], see also [1]). Time resolution is achieved with wavelets by using a scalable modulated window that is shifted along the signal. Hence, generally a small number of wavelets is needed to reconstruct a function with sufficient accuracy. An important property of wavelets is that their mean is zero and their average squared norm is unity. A very well-known example of a wavelet is the Mexican hat and the Morlet wavelet, see Fig. 3. These examples are examples of mother wavelets, which may be dilated and transformed to form the basis. The first wavelet function was developed by Haar (1910).[9] Wavelets have traditionally been used in data analysis to increase the signal-to-noise ratio, and also to compress the data to only a few wavelet functions.
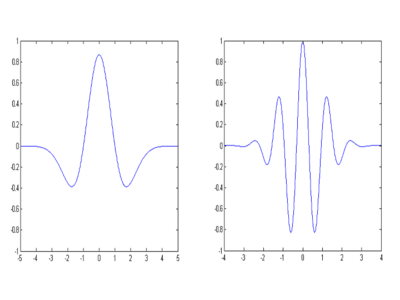
Wavelets were first used in coastal morphodynamics by Sarah Little et al. (1993) [3] to analyze large scale (of the order of 100 to 1000 kms) bathymetric evolution offshore the Hawaian islands; the wavelets the authors adopted for this analysis were Daubechies wavelets, a family of discrete orthogonal wavelets introduced by Ingrid Daubechies (1988)[10]. Thanks to the wavelet scale analysis and application of a wavelet transform, the authors were able to discover a small, low-frequency topographic feature of around 200 kms in length, whose details suggest it is a slow-spreading rift. After this pioneering work, other topography identification investigations have followed (eg. Little et al., 1996[11]). More recently, Li et al. (2005)[3] analyzed nearshore beach profile variability in Duck, North Carolina (USA); the space scales in this case were, instead, of the order of 0.1 kms. The objective of the study was to analyze both time and space variability of the bathymetry. Thus, the authors chose Daubechies’ wavelets as a base and an adapted maximum overlap discrete wavelet transform (AMODWT), as both are very suitable for decomposition of signals with strong space and time variations.
Li et al. (2005)[3] studied in detail a bathymetry profile that has been thoroughly surveyed since 1981. They identified the variance across the profile as nonstationary, with largest variations in the sandbank region; this region occurs between 100 and 400-500 m offshore. Within this region, the 128-256 m spatial scale contained most of the information, and did make the largest contribution to the variance for all the months surveyed. It is worth noting that the largest variations at the 128m scale occurred in the sandbar region, indicating this is the region where the morphology evolves the most, which is to be expected. Contrary to the spatial scales, the temporal wavelets contributed differently to the total variance depending on the month considered and the position along the profile. The two temporal wavelets that span from 32-64 and 64-128 months, respectively, contained most of the variance. Contributions of lower order appeared as large peaks in the profiles, indicating they are mostly event-related, rather than part of the average trend. This is highlighted by the authors with several examples. This work proves wavelets are a useful technique in signal decomposition and have great potential in coastal research.
An example how a signal can be decomposed into different spectral bands using orthogonal wavelets was given by Różyński and Reeve (2005) [12]. Fig. 4, left panel, shows the time series of water level at a Baltic Sea coastal segment in Poland featuring a stormy event on 27th Oct. 2002, sampled at the rate of 0.5 Hz. Next, Fig. 4, right panel, presents the results of wavelet decomposition with the orthogonal Haar wavelet for frequency bands covering wind waves (4 – 8 s), swell (8-16 s) and infragravity waves (16-256 s). We can clearly see the growth of wave height of all those components during the buildup of storm.
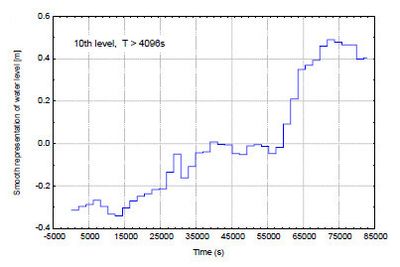
Consequently, Fig. 4, right panel, demonstrates residual spectral bands, which are roughly the same throughout the storm. The patterns belonging to each spectral band are called ‘details’ in wavelet terminology, whereas the pattern in Fig. 5 contains elements with periods above 4096 s i.e. the ultra-slow varying trend, featuring the storm surge. This pattern is called ‘smooth representation’ in wavelet terminology. We can see that the storm was decomposed into spectrally disjoint, orthogonal patterns, allowing for their detailed, individual examination; in wavelet terminology the smooth representation and details together are all parts of multi-resolution analysis of a time series. Jagged trajectories of the smooth representation and details describing low-period variability originate from the use of Haar wavelet; more advanced nearly asymmetric dbN (Daubechies[10]) or nearly symmetric coifN wavelets (also constructed by I. Daubechies) do not produce such artefacts.
Principal Component Analysis (PCA)
Principal Component Analysis is a data analysis method intended to identify the most important patterns in large data sets, i.e. the patterns that represent the most important variance in the data. The PCA method has first been developed by Pearson (1901)[13] and Hotelling (1933)[14].
Consider a dataset [math]\; h(x_i,t_m) = h_{ij}, \; i = 1, .., N_x; \; m = 1, .., N_t \;[/math] consisting of a number of [math]N_t[/math] successive observations of a set of [math]N_x[/math] variables. The most important patterns in the dataset are represented by a limited number of principal components, each representing a pattern of variation in the variables of a certain order of magnitude. The principal component of the first order represents the largest pattern of variation, the principal component of the second order represents the second largest pattern of variation after the first order variation is subtracted, and so on. The essential difference between PCA and data analysis methods such as decomposition according to Fourier or wavelet components is that in this case the principal components are not based on predetermined shape functions, but on shape functions that are derived from the data set itself. This allows the dataset to be rather well reproduced with only a small number of principal components; in practice, two or three principal components are often sufficient.
In PCA the shape functions are not continuous; they are formed by a set of normalized orthogonal weight vectors [math]\; \bf e_k \;[/math] of order [math]\; k = 1,2, .., N_x \;[/math] with each the same number of dimensions [math]N_x[/math] as the set of variables. The elements of these weight vectors are indicated by [math]\; e_{ki} \;[/math] and have the property [math]\; \sum_{i=1}^{N_x} e_{ki} e_{li}= \delta_{kl} \;[/math].
The dataset can be described by a matrix [math]\; \bf D \;[/math] with elements [math]\; d_{im}=h_{i,m} - \overline h_i \;[/math], where [math]\; \overline h_i \;[/math] is the average over all [math]\; m=1, ..,N_t \;[/math] observations. The principal component of order [math]\; k [/math] is represented by the [math]N_t[/math]-dimensional vector [math]\; \bf z_k \;[/math] with elements
[math]\; z_{km} = \sum_{i = 1}^{N_x} \; d_{im} \; e_{ki} . \quad \quad (1)[/math]
The numbers [math]e_{ki}[/math] are the components of the eigenvectors [math]\; \bf e_k [/math] of the [math]N_x*N_x[/math] covariance matrix [math]\; \bf C = D^T D [/math] with elements [math]c_{ij}[/math],
[math]\; c_{ij}=\sum_{m = 1}^{N_t} d_{im} d_{jm}. \quad \quad (2)[/math]
The corresponding eigenvalues [math]\lambda_k[/math] are given by
[math]\sum_{j = 1}^{N_x} \; c_{ij} \; e_{ki} = \lambda_k \; e_{kj} .[/math]
The eigenvalues are positive (because the covariance matrix [math]\; \bf C[/math] is symmetric) and ordered such that [math]\lambda_1 \gt \lambda_2\gt …. \gt \lambda_{Nx}[/math]. The first order principal components [math]\; z_{1j} [/math] describes the greatest pattern of variation in the data set. Routine mathematical procedures can be used to determine the eigenvectors.
The eigenvalues sum up to the total signal variance, i.e. the sum of the terms along the main diagonal of [math]\mathbf C[/math]. They show the distribution of variance among eigenvectors, thus indicating their importance. From a practical point of view several key modes normally contain at least 90% of the total variance, so the most important features of a studied system can be identified. However, it must be emphasized that the principal components are based on correlations, which do not necessarily represent cause-effect relationships.
The first-order principal component is given by
[math]z_{1m} = \sum_{i=1 }^{N_x} \; d_{im} \; e_{1i}. \quad \quad (3)[/math]
The second-order principal component [math]\;\bf z^{(2)} [/math] corresponds to the eigenvector with the second highest eigenvalue of the covariance matrix (2). And so on for the third-order principal component. Most information on the major underlying dynamical processes is often contained in the first two or three principal components.
Before applying PCA, phase shifts between successive datasets (propagating signal) should be removed. A more detailed explanation of the mathematical background of the PCA data analysis methods is given in the Wikipedia article PCA.
Empirical Orthogonal Functions (EOF)
The application of Principal Component Analysis to the analysis of morphological datasets is generally termed EOF, Empirical Orthogonal Functions. EOF methods have been used with success to analyze nearshore beach topography, as will be described below. However, the technique may not be appropriate for studies of bar dynamics as eigenfunctions are fixed in space since bars, on the contrary, are wave-like patterns that travel in time. Extended EOFs and Complex Principal Component Analysis, both modifications of EOFs, do not have such shortcoming; however, they rely on time-lagged data, and thus the data needs to be sampled at constant time intervals. This is not usual in coastal applications, as noted by Larson et al. (2003), but may be achieved via data interpolation.
Larson et al. (2003)[5] cite three papers (Hayden et al. 1975 [15], Winant et al., 1975 [16] and Aubrey et al., 1979[17]) as pioneering applications of EOFs in coastal morphology, in particular for beach profile behavior. These researchers, as Larson et al. (2003) point out, observed that the lower order EOF modes could be related to particular coastal features, i.e. the mean profile, bars and berms, and low-tide terraces to the first, second and third order modes, respectively. Therefore, these studies also constitute first attempts of coastal characterization via EOFs. The EOF method together with a moving window model were used by Wijnberg and Terwindt (1995) [18] to divide the Dutch coast into regions according to their characteristic patterns of behavior. They analyzed 115 kms of Dutch coast via 14 thousand near cross-shore transects at generally 250 m longshore intervals. These regions vary from 5 to 42 kms in size, each characterized mainly by what the authors define as ‘secondary’ features, that is features diverging from the mean profile such as mounds or sandbars (this example and those mentioned below are such that the mean has not been removed from the data). The authors observed sub-decadal shifts of shoreline positions and speculate this could be related to sandbar dynamics. Larson et al. (2003) applied the same technique of Wijnberg and Terwindt (1995) to nearshore topography in a Dutch and a German coastal area. For the Dutch coastal site, the modes were related to the coastal features, with similar results as in Aubrey (1979) except that third EOF was shifted 90 degrees in phase with respect to the second and was also related to the bar system. For the German site, the technique was applied to study beach nourishment effects on topography evolution at a beach resort that has suffered from severe erosion in the past (Dette and Newe, 1997).[19] In this case the first EOF indicated an increase in mean elevation. Similarly to other EOF analysis at other sites infilled sites, rapid changes occur at the beginning and were then followed by gradual adjustment to an equilibrium. In general the process takes one year if beach nourishment is nearshore, or considerably longer if the beach nourishment is at the berm, as Larson et al. (2003) observed.
Mathematical procedure
Some key mathematical details of the EOF analysis method of two-dimensional spatial data are presented below. In sum, it should be underlined that the EOF, as well as the Singular Spectrum Analysis (SSA), Extended EOF (EEOF) and Multi-channel SSA (MSSA) methods, are all variants of the same PCA methodology, based on the covariance structure of a studied system.
In the EOF variant the system matrix is composed of covariances of a studied parameter/quantity at two points of the domain at the same moments in time. For example, when the seabed is sampled [math]N_t[/math] times, the measurements usually consist of [math]N_y[/math] cross-shore profiles with [math]N_x[/math] sampling points in each of them. The dataset is described by a matrix [math]\; \bf D \;[/math] with elements [math]\; d_{im}=h_{i,m} - \overline h_i \;[/math], where [math]\; \overline h_i \;[/math] is the average over all [math]\; m=1, ..,N_t \;[/math] observations. The resulting lag-0 covariance matrix [math]\mathbf C[/math] with elements [math]c_{i,j}[/math] has [math]N_{xy}=N_x*N_y[/math] terms, where [math]N_{xy}[/math] is the number locations of the data grid:
[math]c_{i,j} = \sum_{m=1}^{N_t} \; d_{im} d_{jm} , \quad \quad (4)[/math]
with [math]i,j = 1, .... , N_{xy}[/math]. Note that this is identical to Eq. (2). Each index value [math]i[/math] corresponds to a particular point of the [math]N_x*N_y[/math] data grid, and the same holds for each [math]j[/math]. For [math]i=j[/math] (main diagonal) the terms represent variances. The eigenvectors [math]\mathbf e_k[/math] and eigenvalues [math]\lambda_k[/math] are defined by
[math]\sum_{j=1}^{N_{xy}} c_{ij} e_{kj} = \lambda_k e_{ki} ,\; i=1, ..n.[/math]
The eigenvectors [math]\mathbf e_k[/math] are orthogonal and scaled to unit length, [math]\sum_{j=1}^{N_{xy}} e_{kj} e_{lj} = \delta_{kl}[/math] and the eigenvalues ranked in decreasing order of magnitude. The vectors [math]\mathbf e_k[/math] represent the spatial side of the EOF decomposition; when plotted in the real physical space (e.g. the studied seabed domain), the components [math]e_{ki}[/math] indicate the areas of highest variability.
The principal components [math]\mathbf z_k, \; k=1, .., N_{xy}[/math] (temporal side of EOF decomposition) can be obtained using the following projections:
[math]z_{km}=\sum_{i=1}^{N_{xy}} \; d_{im} \; e_{ki} , \quad \quad (5)[/math]
where [math]z_{km}[/math] denotes the [math]m[/math]-th moment in time ([math]m=1, .., N_t[/math]) of the [math]k[/math]-th principal component [math]\mathbf z_k[/math], associated with the [math]k[/math]-th eigenvector [math]\mathbf e_k[/math]. Very importantly, its variance is equal to [math]\lambda_k[/math]. As for principal component analysis, each pair [math]\mathbf z_k[/math] and [math]\mathbf e_k[/math] provides information on the spatiotemporal evolution of the [math]k[/math]-th EOF mode.
Singular Spectrum Analysis (SSA)
A particular modification of PCA, namely Singular spectrum analysis (SSA), has been used to identify chaotic properties of a system, that is, to determine the number (embedding dimension) of independent variables that are needed to describe the system, and the properties of the attractors in such system. SSA was extensively discussed by Southgate et al. (2003[20]), and the main points raised by the authors are summarized here. Firstly, in the case of SSA the data matrix has in its columns not the full original measured time series, but the data at successive equitemporal lags, up to the maximum shift needed for a full system’s description. The number of columns of the data matrix defined as such is called the embedding dimension, [math]M[/math], and the SSA will not resolve periods longer than that corresponding to [math]M[/math]. It is of interest to note that the SSA technique is used not only for chaotic characterization studies, but also for noise reduction, data detrending, oscillatory characterization, or forecasting. Example applications to coastal morphology, given by Southgate et al. (2003[20]), relate to long-term shoreline evolution. However, in general this technique has not been applied to coastal research, but rather to climatology (e.g. Ghil et al., 2002 [21]).
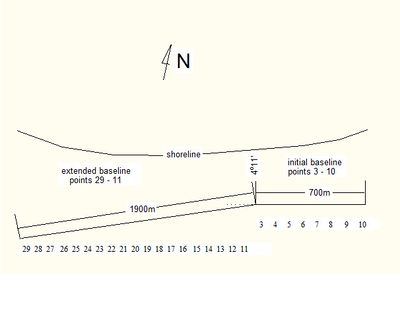
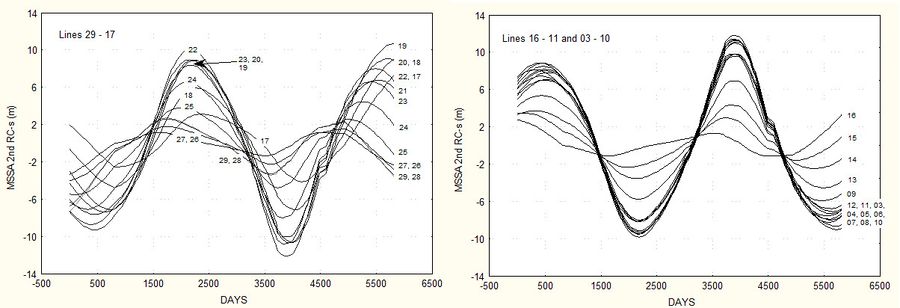
EOF can be generalized to Extended EOF (EEOF) for data sets containing many spatial points and few time realizations. For data sets where the number of spatial points is less than the number of realizations SSA can be generalized to Multi-channel SSA (MSSA). An example of application of the MSSA method was presented by Różyński (2005) [22], who analyzed shoreline variations from 1983 until 1999, sampled monthly at 27 equally spanned transects, covering a stretch of 2,600 m of an open sea coastal segment in Poland, transects 29-11 and 03-10, see Fig. 6. The study revealed three important patterns representing shoreline standing waves. Upon locations of their nodes, the wavelengths of those standing waves could be directly evaluated. Next, the magnitudes of the variation of antinodes were used for the assessment of their amplitudes. Finally, the periods were established by determination of time needed by antinodes to evolve from maximum seaward to maximum landward position. The largest standing wave had the wavelength of 1,500 m with amplitudes ranging between 4 and 20 m about the mean shoreline position at a given transect and the corresponding period of more than 32 years, see Fig. 7. No firm explanation for the existence of that wave could be provided. Physical mechanisms that may produce standing shoreline waves are discussed in the article Rhythmic shoreline features.
The 2nd wave had the wavelength in the range of 1,000-1,400 m, amplitudes of 10 m and the period of 8 years, see Fig. 8. Later studies, Różyński (2010) [23] and Różyński (2015) [24], identified a coupling of this standing wave to variations of the winter index of North Atlantic Oscillation (for Dec., Jan., Feb. and Mar.), which contains a significant component with the period of 8 years and was found to be controlling winter wave climates and water levels in the Baltic Sea to a considerable degree.
The 3rd standing wave was found to be less regular; the estimated wavelength fell between 1,400 – 1,600 m, the amplitudes varied from 10 m at one anti-node to only 6 m at the other, see Fig. 9. The processes responsible for the presence of this wave could not be identified in the absence of records of long-term hydrodynamic background.
Mathematical procedure
In the SSA method the spatial dimension is reduced to a single point: [math]N_x N_y = 1[/math]. The focus is on analyzing the temporal variation in the observed time series [math]d_n = h_n -\overline h, \; n=1, .., N[/math] from which the temporal average [math]\overline h = 0[/math] has been removed. For this purpose, the lagged covariance matrix is built:
[math]\mathbf{C} = \begin{bmatrix} c(0) & c(1) & c(2) & \cdots & c(M-1) \\ c(1) & c(0) & c(1) & \cdots & c(M-2) \\ \vdots & \vdots & \vdots & & \vdots \\ c(M-1) & c(M-2) & c(M-3) & \cdots & c(0) \end{bmatrix} [/math]
with the terms:
[math]c(n)=\frac{1}{N - n} \sum_{m=1}^{N-n} \; d_m \; d_{m+n} , \quad \quad (6)[/math]
where [math]d_n[/math] is the value of [math]d[/math] at time [math]t_n[/math]. The parameter [math]M[/math] is called either window length or embedding dimension and determines the maximum covariance lag; a practical rule of thumb suggests that [math]M \le N/3 \;[/math] ([math]N[/math] is the total number of successive observations). The matrix [math]\mathbf C[/math] is symmetrical and has positive eigenvalues; if one or more eigenvalues are zero then the signal contains a deterministic component, represented by a perfect sine function. Formally, we can compute the orthonormal eigenvectors [math]\mathbf e_k[/math] and principal components [math] \mathbf{z_k}[/math] of this matrix. The latter are derived from the formula:
[math]z_{k,n}=\sum_{m=1}^{M} \; d_{m+n-1} \; e_{km}[/math] for [math]1 \le n \le N-M +1 . \quad \quad (7)[/math]
Thus, we have to take [math]M[/math] elements of the original series [math]\mathbf d[/math] from [math]m[/math]-th to [math](m+M)[/math]-th element, compute their products with the corresponding elements of the eigenvectors [math]\mathbf e_k[/math] of the matrix [math]\mathbf C[/math] and sum these products to obtain the [math]n[/math]-th element of the [math]k[/math]-th principal component. Hence, the principal components are time series of the length [math]N – M[/math]. Importantly, despite being orthogonal, the prinicipal components are not correlated only at lag zero. Because [math]M[/math] consecutive elements of the original series are needed to compute one term of every principal component, the correlation structure of the original series must be imprinted in the principal components. Moreover, there may be up to [math]M[/math] subsets of the original time series containing the specific element [math]d_{m+n}[/math], so there may be up to [math]M[/math] different ways of reconstructing this element with principal components:
[math]d_n=\sum_{k=1}^{M} \; z_{k,n-m+1} \; e_{km} , \qquad (8)[/math]
with [math]1 \le n \le N, \; 1 \le n-m+1 \le N-M+1 .[/math] (Relation (8) is obtained through multiplication of (7) by [math]e_{km'}[/math], summing over [math]k[/math], using [math]\sum_{k=1}^M e_{km} e_{km'} = \delta_{mm'}[/math] and changing indices [math]m+n-1 \longrightarrow n[/math]). Thus, using principal components we do not obtain a unique expansion of the original series. However, uniqueness can be established when we calculate the mean values of all possible ways of reconstructing the original signal:
[math] d_{k,n} =\frac{1}{M} \sum_{m=1}^{M} \; z_{k,n-m+1} \; e_{km} \qquad (9)[/math]
for [math]M \le n \le N – M +1[/math] at the middle part of the signal,
[math] d_{k,n} =\frac{1}{n} \sum_{m=1}^{n} \; z_{k,n-m+1} \; e_{km} \qquad (10)[/math]
for [math]1 \le n \le M -1[/math] at the beginning of the signal,
[math] d_{k,n} =\frac{1}{N - n +1} \sum_{m=n - N + M}^{M} \; z_{k,n-m+1} \; e_{km} \qquad (11)[/math]
for [math]N-M +2\le n \le N [/math] at the end of the signal.
There are [math]M[/math] quantities [math]\mathbf d_k[/math], which are termed reconstructed components and provide a unique expansion of the original signal. They are additive, but not orthogonal, so their variances are not cumulative. Therefore, a researcher should investigate not only single reconstructed components, but also their subsets in search for plausible interpretation of signal constituents. Traditional time series analysis techniques, mostly the Fourier analysis are used for this purpose. Usually, the entire useful information is contained in a few reconstructed components, so the analysis is not as tedious as might be suspected.
Finally, both the EEOF and MSSA methods provide unique expansions of the studied signals in time and space as well. Both methods are identical and differences in terminology are mostly practical; the term EEOF is used when [math]N_{xy} \equiv N_x *N_y \gg N_t[/math], whereas MSSA is referred to when [math]N_t \gt N_{xy}[/math]. The resulting block system matrix is presented below:
[math]\mathbf{T} = \begin{bmatrix} T_{1,1} & T_{1,2} & \cdots & T_{1, N_{xy}} \\ T_{2,1} & T_{2,2} & \cdots & T_{2, N_{xy}} \\ \vdots & \vdots & \ddots & \vdots \\ T_{ N_{xy}, 1} & T_{ N_{xy}, 2} & \cdots & T_{ N_{xy}, N_{xy}} \end{bmatrix} [/math]
The main diagonal contains auto-covariance matrices of all [math]N_{xy}[/math] signals involved, the remaining (block) terms represent cross-covariances among them. Formally, this matrix can be manipulated analogously to previous description, so that [math]M[/math] reconstructed components are obtained. However, we should keep in mind that their interpretation can be difficult, because of the number of spatial points considered. Therefore, caution is recommended when applying these advanced techniques; such analysis should be preceded by ordinary EOF/SSA studies, depending on the problem studied.
Principal Oscillation Patterns and PIP
In a Principal Oscillation Pattern (POP) analysis the data is analyzed using patterns based on approximate forms of dynamical equations, so it may be used to identify changing patterns, such as standing waves and migrating waves (Larson et al, 2003)[5]. POP is a linearized form of the more general Principal Interaction Pattern (PIP) analysis. A POP analysis using the long-term Dutch JARKUS dataset of cross-shore beach profiles (Jansen, 1997[25]) showed that POP systematically lost 4% to 8% more data than an EOF analysis. The prediction method was optimised using 8 POPs as adding more POPS included more of the noise. Różyński and Jansen (2002)[26] applied POP analysis to 4 beach profiles at Lubiatowo (Poland) and recommended that an EOF analysis be carried out first.
Appendix A: Linear regression theory
Although regression analysis is explained in many textbooks, a short mathematical introduction is given below. The object of linear regression is to analyze the correlation of a measurable property [math]h[/math] (the so-called 'dependent variable' or 'target') with a number [math]K-1[/math] measurable factors [math]y_k, \; k=2, .., K[/math] (the 'independent variables' or 'regressors'). Linear regression is based on the assumption that [math]h[/math] can be estimated through a linear relationship:
[math]h = \hat{h} +\epsilon \; , \quad \hat{h} = a_1 + \sum_{k=2}^K a_k y_k = \sum_{k=1}^K a_k y_k \; , \qquad (A1)[/math]
where [math]\hat{h}[/math] is the estimator, [math]a_k, \; k=2, .., K[/math] are the regression coefficients, [math]a_1[/math] is the intercept and [math]y_1=1[/math]. The term [math]\epsilon[/math] is the 'error', i.e., the difference between the true value [math]h[/math] and the estimator [math]\hat{h}[/math]. (Note: Linear regression means linear in the regression coefficients; the regressors [math]y_k[/math] can be nonlinear quantities, for example [math]y_3=y_2^2[/math].) Now assume that we have observations of [math]N[/math] different instances of the [math]K-1[/math] regressors, [math]y_{ki}, \; i=1, .., N[/math], and corresponding observations of the dependent variable, [math]h_i[/math]. If [math]N\gt K[/math] these observations can be used to estimate the values of the regression coefficients [math]a_k[/math] by looking for the best solution to the linear system
[math]h_i = \sum_{k=1}^K a_k y_{ki} + \epsilon_i \; , \qquad (A2)[/math]
where [math]\epsilon_i[/math] are errors related to: (i) the approximate validity of the linear estimator (sometimes called 'epistemic uncertainty') and (ii) measurement inaccuracies, which are often statistical ('aleatoric') uncertainties. The errors are considered to be stochastic variables with zero mean, [math]E[\epsilon_i]=0[/math] and variance [math]\sigma_i^2 \equiv E[\epsilon_i^2][/math] (we use the notation [math]E[x][/math]= the mean value from a large number of trials of the stochastic variable [math]x[/math]).
What is 'the best solution"? Different criteria can be used. Least square optimization is the most often used criterium, i.e., the solution for which the sum of the squared errors [math]\Phi[/math] is minimum,
[math]\Phi = ½ \sum_{i=1}^N \epsilon_i^2 = ½ \sum_{i=1}^N \sum_{j=1}^N \big(h_i - \sum_{k=1}^K a_k y_{ki}\big) \big(h_j - \sum_{k'=1}^K a_{k'} y_{k'j}\big) . \qquad (A3)[/math]
At minimum, [math]\Phi[/math] increases for any change in one of the coefficients [math]a_k[/math], which implies that the partial derivatives are zero:
[math]\Large\frac{\partial \Phi}{\partial a_k}\normalsize = 0 , \; k=1, ..,K . \qquad (A4)[/math]
This condition yields the set of [math]K[/math] linear equations
[math] - \sum_{i=1}^N y_{ki} h_i + \sum_{i=1}^N \sum_{k'=1}^K y_{ki} y_{k'i} a_{k'} = 0 . \qquad (A5)[/math]
from which the regression coefficients [math]a_k[/math] can be solved.
In the more compact matrix notation we may write: [math]H[/math] is the [math]N[/math]-vector with elements [math]h_i[/math], [math]\; A[/math] is the [math]K[/math]-vector with elements [math]a_k[/math] and [math]Y[/math] is the [math]K \times N[/math] matrix with elements [math]y_{ki}[/math]. The linear equations (A5) can then be written
[math]Y^T \, H = Y^T \, Y \, A . \qquad (A6)[/math]
The solution is found by inversion of the [math]N \times N[/math] matrix [math]Y^T \, Y[/math], giving
[math]A = (Y^T \, Y)^{-1} Y^T \, H . \qquad (A7)[/math]
Least squares is the best solution if the regressors [math]y_k[/math] are uncorrelated and if the errors [math]\epsilon_i[/math] are uncorrelated and identically Gaussian-distributed, i.e., they all have the same variance [math]\sigma_i^2[/math]. This is often not the case in practice. A few other cases are discussed below.
Case 1. The data have errors that scale with their magnitude. Then a log transform of the data produces errors approximately independent of the magnitude. Linear regression with least squares is applied to the log-transformed data.
Case 2. The errors differ among the data ('non-homoscedasticity'), [math]\sigma_i \ne \sigma_j , \, i \ne j[/math]. If estimates of the variances are known, one can use weighted least squares instead of least squares, i.e., replace (A3) with [math]\Phi = ½ \sum_{i=1}^N \big( \epsilon_i / \sigma_i \big)^2[/math].
Case 3. Multicollinearity, meaning a linear relationship exists between two or more regressor variables. In this case the non-independent regressor variable should be removed from the data.
Case 4. The errors of the [math]N[/math] observations are correlated, [math]c_{ij} \equiv E[\epsilon_i \, \epsilon_j] \ne 0[/math]. If an estimate of the covariances [math]c_{ij} [/math] is known, the generalized least squares method can be used. The solution (A7) is then replaced by
[math]A = (Y^T \, C^{-1} \, Y)^{-1} Y^T \, C^{-1} H , \qquad (A8)[/math]
where [math]C[/math] is the covariance matrix with elements [math]c_{ij}[/math]. Another option is to use kriging, see the article Data interpolation with Kriging.
Related articles
References
- ↑ Gilmore, R. and Lefranc, M. 2003. The topology of chaos: Alice in Stretch and Squeezeland, first edition, Wiley-VCH Verlag GmbH and Co, Switzerland.
- ↑ Rattan, S.S.P, Ruessink B.G., and Hsieh W. W. 2005. Non-linear complex principal component analysis of nearshore bathymetry. Nonlinear Processes in Geophysics: 12, 661–670
- ↑ 3.0 3.1 3.2 3.3 Li, Y., Lark, M. and Reeve, D. 2005. Multi-scale variability of beach profiles at Duck: A wavelet analysis. Coastal Engineering 52: 1133-1153 Cite error: Invalid
<ref>tag; name "L" defined multiple times with different content - ↑ 4.0 4.1 4.2 Southgate, H. N., Wijnberg, K. M., Larson, M., Capobianco, M. and Jansen, H. 2003. Analysis of field data of coastal morphological evolution over yearly and decadal timescales. Part 2: Non-linear techniques. Journal of Coastal Research 19: 776-789. Cite error: Invalid
<ref>tag; name "S" defined multiple times with different content - ↑ 5.0 5.1 5.2 5.3 Larson, M., Capobianco, M., Jansen, H., Rozynski, G. N., Stive, M., Wijnberg, K. M. and Hulscher, S. 2003. Analysis and modeling of field data on coastal morphological evolution over yearly and decadal time scales. Part 1: Background and linear techniques. Journal of Coastal Research 19: 760-775
- ↑ Genz, A.S., Fletcher, C.H., Dunn, R.A., Frazer, L.N. and Rooney, J.J. 2007. The predictive accuracy of shoreline change rate methods and alongshore beach variation on Maui, Hawaii. Journal of Coastal Research 23(1): 87 – 105
- ↑ Sutherland, J., Peet, A.H. and Soulsby, R.L. 2004. Evaluating the performance of morphological models. Coastal Engineering 51, pp. 917-939.
- ↑ Burrus, C. S., R. A. Gopinath and Guo, H. 1998. Introduction To Wavelets And Wavelet Transforms, A Primer. Prentice Hall, USA.
- ↑ Haar A. 1910. Zur Theorie der orthogonalen Funktionensysteme, Mathematische Annalen 69: 331-371
- ↑ 10.0 10.1 Daubechies I. 1988. Orthonormal Bases Of Compactly Supported Wavelets. Communications on Pure and Applied Mathematics 41: 909-996
- ↑ Little, S. A. and Smith, D.K. 1996. Fault scarp identification in side-scan sonar and bathymetry images from the mid-atlantic ridge using wavelet-based digital filters. Marine Geophysical Researches 18: 741-755
- ↑ Różyński, G., Reeve, D. 2005. Multi-resolution analysis of nearshore hydrodynamics using discrete wavelet transforms. Coastal Engineering 52: 771-792
- ↑ Pearson, K. 1901. On Lines and Planes of Closest Fit to Systems of Points in Space. Philosophical Magazine. 2 (11): 559–572
- ↑ Hotelling, H. 1933. Analysis of a complex of statistical variables into principal components. Journal of Educational Psychology, 24, 417-441, and 498-520
- ↑ Hayden, B., Felder, W., Fisher, J., Resion, D., Vincent, L. and Dolan, R. 1975. Systematic variations in inshore bathymetry. Technical report No. 10, Department on Environmental Sciences, University of Virginia, Virginia, USA.
- ↑ Winant, C. D., Inman, D. L. And Nordstrom, C. E. 1975. Description of seasonal beach changes using empirical eigenfunctions. Journal of Geophysical Research 80: 1979-1986
- ↑ Aubrey, D. G., Inman, D. L. and Winant, C. D. 1979. Seasonal patterns of onshore/offshore sediment movement. Journal of Geophysical Research 84: 6347-6354
- ↑ Wijnberg K. M. and Terwindt J. H. J. 1995. Extracting decadal morphological behavior from high-resolution, long-term bathymetric surveys along the Holland coast using eigenfunction analysis. Marine Geology 126: 301-330
- ↑ Dette, H. H. and Newe, J. 1997.Depot beach fill in front of a cliff. Monitoring of a nourishment site on the Island of Sylt 1984-1994. Draft Report, Leichweiss Institute, Technical University of Braunschweig, Braunschweig, Germany.
- ↑ 20.0 20.1 Southgate, H.N., Wijnberg, K.M., Larson, M., Capobianco, M. and Jansen, K. 2003. Analysis of Field Data of Coastal Morphological Evolution over Yearly and Decadal Timescales. Part 2: Non-Linear Techniques. Journal of Coastal Research 19: 776–789
- ↑ Ghil M., R. M. Allen, M. D. Dettinger, K. Ide, D. Kondrashov, M. E. Mann, A. Robertson, A. Saunders, Y. Tian, F. Varadi, and Yiou, P. 2002. Advanced spectral methods for climatic time series. Reviews in Geophysics 40: 3.1-3.41
- ↑ Różyński, G. 2005. Long term shoreline response of a non-tidal, barred coast. Coastal Engineering 52: 79-91
- ↑ Różyński, G. 2010. Long-term evolution of Baltic Sea wave climate near a coastal segment in Poland; its drivers and impacts. Ocean Engineering 37: 186-199
- ↑ Różyński, G. 2015. Long-term couplings of winter index of North Atlantic oscillation and water level in the Baltic Sea and Kattegat. Ocean Engineering, 109: 113–126
- ↑ Jansen, H. 1997. POP analysis of the JARKUS dataset: the IJmuiden-Katwijk section. Fase 2 Report, Project RKZ-319, Delft Univ. Technology, Netherlands.
- ↑ Różyński, G. and Jansen, H. 2002. Modeling Nearshore Bed Topography with Principal Oscillation Patterns. J. Wtrwy., Port, Coast., and Oc. Engrg. 128: 202-215
Please note that others may also have edited the contents of this article.
|